ChemAurum 化学与物理的碰撞 2024-02-23 11:07 陕西
众所周知，随着共轭体系的增大，分子吸收波长往往越长，换言之，随着电子在分子中离域程度的增加，吸收波长也相应增加。拿最简单的共轭多烯而言，随着共轭双键数目增加，吸收光谱从紫外区慢慢移动到可见光区。
从形象上讲，当两个双键从孤立转为共轭状态时，形成了能量更高的HOMO和能量更低的LUMO，因此造成分子带隙减少，吸收光谱红移。这一结论与熟知的Woodward-Fieser经验规则相符。从Hückel 分子轨道理论的角度看，写出分子的久期行列式就能对应的得到轨道的系数，从而获得分子轨道的能量：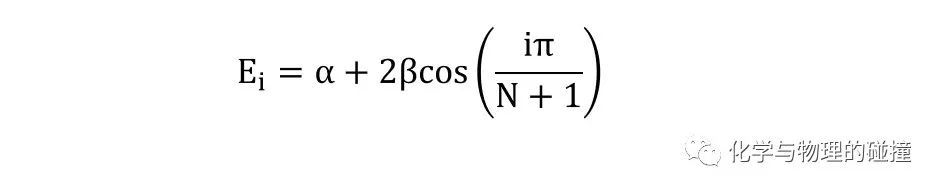
从这个能量表达式可见，对于共轭多烯而言共轭的双键数目越多，分子带隙也就越小。而根据势箱理论，共轭多烯的光吸收可以看作是在一维箱中运动的电子在最低能级和第一激发态的跃迁，而箱中粒子的运动满足薛定谔方程，令势阱无限深，即电子限定在分子Π轨道内部运动。
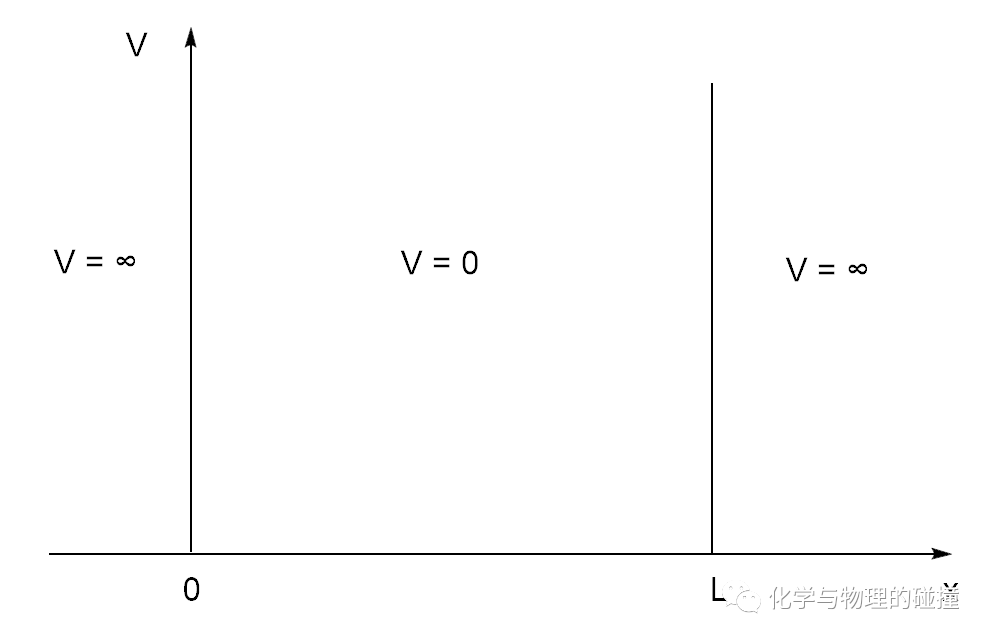
在x<0和x>L处求解薛定谔方程Hψ=Eψ，由于V=∞，那么ψ=0，即电子被限制在0~L之间运动。而在0<x<L处求解薛定谔方程：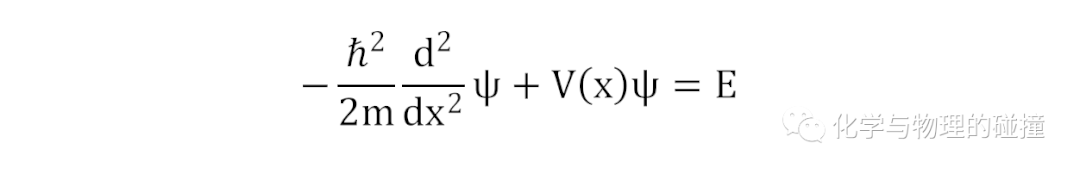
考虑到波函数的连续性，ψ0=0，ψL=0，带入通解ψ=Asin(kx)，归一化的解是: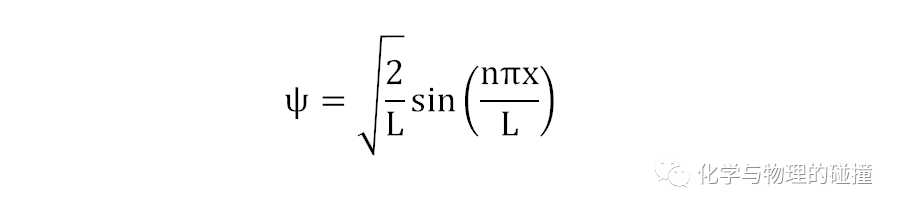
注意，这里波函数的波长并不能等同于光吸收的波长，光吸收的波长满足：E=hc/λ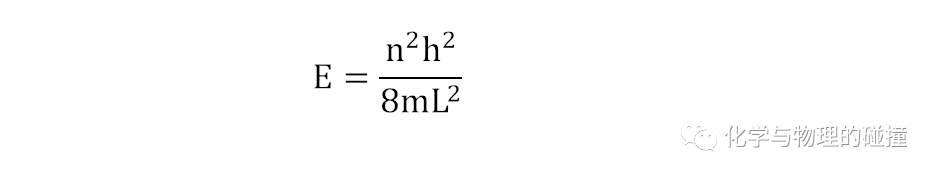
可见分子从基态n=1到第一激发态n=2的能量差随着L的增加而减少，根据波长和能量的关系，可知：
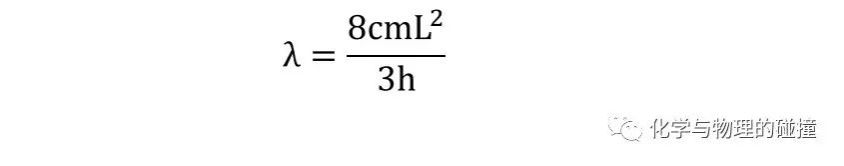
从上面的结果不难看出，电子的离域范围越大，能量就越低，因而分子的光吸收波长就越长。
