1 阿贝衍射极限
19 世纪末,恩斯特・阿贝(Abbe, 1873)与瑞利勋爵(Rayleigh, 1896)提出了显微镜领域广为人知的 “衍射极限” 概念。简单来说,这一极限意味着:无法分辨结构中两个间距小于约半个波长(λ)的单元;在横向(x,y)平面中是如此,到了纵向(z)平面,可分辨的最小距离则会更大。换句话说,根据阿贝判据,横向平面中可分辨的最小距离(δxmin、δymin)可近似表示为:(δxmin,δymin)≈λ/2
衍射极限还带来另一个结果:无法将激光束聚焦到尺寸小于约λ/2的光斑(见图 1)。
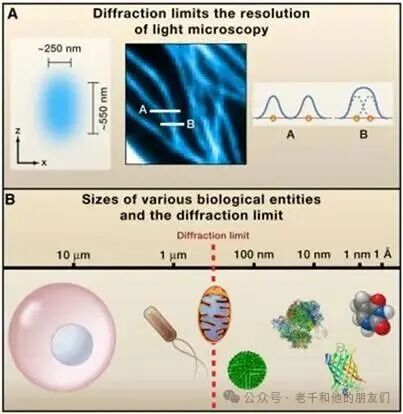
图 1:A 图:(左)聚焦激光束,(中)研究对象结构,(右)可分辨(A)与不可分辨(B)的结构特征;B 图:从左至右依次为哺乳动物细胞、大肠杆菌细胞、线粒体、流感病毒、核糖体、绿色荧光蛋白(GFP)、胸腺嘧啶。
光学显微镜(简称 “光镜”)与电子显微镜同为生物结构成像的核心工具,但对光镜而言,衍射极限造成了明显限制 —— 若两个物体的间距在 400/2=200 纳米(远蓝光波段)到 700/2=350 纳米(远红光波段)之间,便无法被分辨。电子显微镜的波长远小于光镜,因此不存在这一问题,但它很难用于活细胞成像。
大肠杆菌细胞的尺寸约为 1000 纳米(即1微米),虽略大于衍射极限,但二者数量级相近(见图 1)。这也解释了为何过去难以清晰成像活细菌的内部结构细节,甚至一度让人们误以为细菌是“结构简单的原始生物”,几乎没有复杂的内部构造。
阿贝极限的更精确定义,可依托荧光显微镜的点扩散函数(PSF)展开。具体来说,当荧光从一个点光源发出时,受阿贝衍射极限影响,荧光会在空间中扩散,最终在显微镜的像平面上呈现为近似高斯函数的分布。点光源(狄拉克函数)的傅里叶变换在整个频率谱中是均匀的,而点扩散函数的傅里叶变换会随频率升高而减弱,在 x、y 两个方向的空间频率1/Δmin处降至零(见图 2)。
什么是傅里叶变换?
通俗的说,傅里叶变换理解成 “拆细节”:比如一张照片里,蓝天、人脸轮廓是 “粗细节”(低频信息),头发丝、衣服纹理是 “细细节”(高频信息),傅里叶变换就是把图像拆成不同粗细的细节,告诉你每种细节的信息量。
对理想点光源来说,它本身包含了从 “极粗” 到 “极细” 所有细节,所以它的傅里叶变换在整个频率谱里是均匀的。但实际成像的 “模糊斑(PSF)” 不一样,它的傅里叶变换会随着细节变细(频率升高)而减弱 —— 比如到了 “头发丝级” 的中高频细节,信息就变少了,成像会模糊;等到 “1/Δmin” 这个特定的高频(对应极细的细节)时,信息直接降到零,意思是显微镜根本 “传不动” 这么细的细节了。
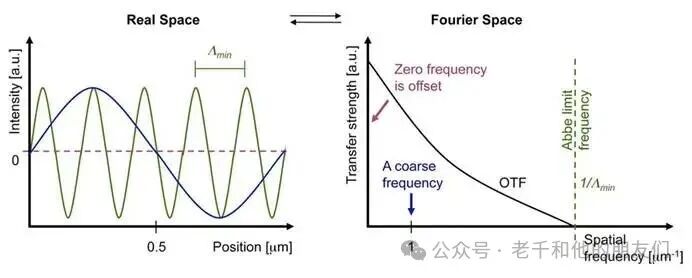
图 2:左图:高频(绿色)与低频(蓝色)空间频率波;右图:点扩散函数(PSF)的对应傅里叶变换,即低频(1)与高频(1/Δmin)波的光学传递函数(OTF)。
由于任何物体图像的傅里叶变换,等于物体本身的傅里叶变换与显微镜点扩散函数傅里叶变换的乘积,因此长度Δmin定义了显微镜的结构分辨率极限(Schermelleh,2010)。若以这一参数客观定义阿贝极限,横向平面中的阿贝极限与显微镜基本参数的关系可表示为:
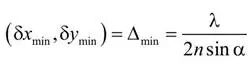
在标准光学显微镜中,轴向(z 方向)的分辨率通常更差,其近似表达式为(Born & Wolf, 2002):
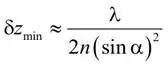
式中,α为观察点光源时的半孔径角,n为显微镜所用介质的折射率。上述第一个公式量化了横向平面中的阿贝极限,科研人员也一直致力于优化公式中的各项参数,以突破这一限制。
2 早期突破光学显微镜衍射极限的尝试
早期尝试突破阿贝极限的思路,大致可归为远场与近场两类方法。
远场方法
通过共聚焦显微镜(Cremer & Cremer, 1978)与多光子显微镜(Hell & Stelzer, 2002),研究人员实现了分辨率的提升。这两种技术不仅能有效抑制背景噪声,也为后续单分子光谱学的发展奠定了基础。4Pi 显微镜(Hell & Stelzer, 2002)与I5M显微镜(Gustafsson,1995)则大幅改善了轴向分辨率差的问题——它们通过使用两个物镜,在三维空间中形成近乎球形的聚焦光斑,从而突破轴向限制。
另一种方法是结构光照明显微镜(SIM),其核心是利用两束光的干涉,在激发光中形成正弦图案(Heintzmann & Cremer, 1999)。当这种正弦波与研究对象相互作用时,会产生莫尔条纹,原本小于衍射极限的空间细节便会通过条纹显现;只要发射的荧光强度与激发光强度呈线性关系,这种方法就能将阿贝极限的分辨率提升一倍。
这些远场方法虽能将横向平面的分辨率提升至阿贝极限的两倍,也能通过双物镜增大仪器孔径角,显著改善轴向分辨率,但本质上仍未脱离阿贝极限的基本约束 —— 它们只是 “拓展” 了极限,而非真正 “突破”。
近场方法
全内反射荧光(TIRF)是荧光光谱学与显微镜领域中应用广泛的技术(Ambrose, 1956;Axelrod, 1981)。当光以大倾角相对于玻璃-介质界面发生全反射时,会产生倏逝波(evanescent wave);这种波只能穿透介质约 100 纳米,刚好可用于激发界面附近极小体积内的荧光分子。
什么是倏逝波?
很多人以为 “全反射就是光完全不进光疏介质”,但其实不是 —— 此时会有极少量光 “渗” 进光疏介质,但只贴在界面附近(比如之前提到的 100 纳米左右),而且离界面越远,光的强度会飞速减弱,几乎瞬间消失(“倏逝” 就是 “很快消失” 的意思)。这种“贴在界面、转瞬即逝的薄光”,就是倏逝波。
这种方法虽能大幅提升轴向分辨率,但其应用范围严格局限于近表面研究 —— 无法对完整细胞的内部结构进行成像。
近场扫描光学显微镜(NSOM,又称 SNOM)在理论上可无限突破阿贝极限。它无需物镜,而是通过一个窄孔径(如锥形玻璃光纤的末端)发出的光,在极近的距离内照射研究表面。借助这一技术,倏逝波在横向与轴向的范围均被限制在 20 纳米以内,在所有维度上都将阿贝极限突破了一个数量级(Betzig & Trautmann, 1992)。通过精细的技术操作,研究人员还成功用它检测到单个荧光团,为单分子显微镜的实现提供了可能(Betzig,1993)。
尽管成果显著,但这种技术的操作难度大,应用也始终局限于表面研究。真正推动超分辨荧光显微镜突破的,是后来出现的两类远场激发技术——下文将详细介绍。
3 超分辨荧光显微镜的发现
迄今为止,已有两种远场原理能实现基于荧光的显微镜成像,且分辨率远超阿贝极限。第一种被称为 “超分辨集合荧光团显微镜”,第二种则是 “超分辨单荧光团显微镜”。
第一种原理的核心是 “受激发射损耗(STED)”—— 通过受激发射,耗尽样品中除研究对象某一小区域外所有分子的荧光。在饱和受激发射的条件下,这个 “活性发光区域” 的尺寸可变得远小于衍射极限。只要将定义该区域的光斑在研究对象上扫描,并持续监测荧光发射,就能通过计算机重建出物体的图像(Hell, 2000)。
这一原理也可通过饱和结构光照明显微镜(SSIM)实现(Gustafsson, 2005)。这类方法既适用于荧光区域包含多个荧光团的情况,也适用于单个荧光团的情况,因此统称为 “超分辨集合荧光团显微镜”。它们的共同特点是:SSIM 中激发峰的饱和、STED 中受激发射的饱和,都能产生远高于阿贝极限允许的空间频率(见图 2)。
这一原理的发现分两个阶段:先是对方法的理论描述,再是实验验证与实现。
第二种原理则基于一个关键认知:在给定时间内,从物体上探测到的几乎所有光子,都来自单个荧光团,且这些荧光团之间的间距大于阿贝极限(见公式 1)。
利用这一特点,研究人员可估算出发射点光源的位置,精度远高于阿贝衍射极限。
这类方法统称为 “超分辨单荧光团显微镜”,其发展可分为三步:首先是在致密介质中发现单荧光团光谱学,接着是对原理的理论描述,最后是实验实现。
3.1 超分辨集合荧光团显微镜:STED 及其衍生技术
20 世纪 90 年代初,斯特凡・黑尔(Stefan Hell)以博士后身份从德国前往芬兰图尔库大学 —— 他希望能找到合适的环境,验证自己当时颇具争议的想法:在远场光学显微镜中,不仅有可能突破阿贝衍射极限,而且这种突破具备可行性。
他在两篇理论论文中,详细阐述了 “受激发射损耗(STED)显微镜” 这一开创性概念的原理,并从定量角度明确了实验条件(Hell & Wichmann, 1994),同时还介绍了类似技术(Hell & Kroug, 1995)。回到德国后,他终于组装出一台足够精密的荧光显微镜,成功为 STED 显微镜的原理提供了实验验证。
STED 显微镜用到两束激光:一束是低强度激光,用于照射标记研究对象结构的荧光团,这束光的聚焦区域较宽,尺寸受阿贝衍射极限限制;另一束是高强度 STED 激光,波长比第一束红移,其聚焦区域中心有一个强度为零的 “暗点”,强度从暗点向四周递增。这束 STED 激光能快速将被第一束激光激发的荧光团,从第一激发单线态(S1)的振动基态,降至电子基态的高振动能态,随后这些荧光团会迅速跃迁到振动基态(见图 3)。
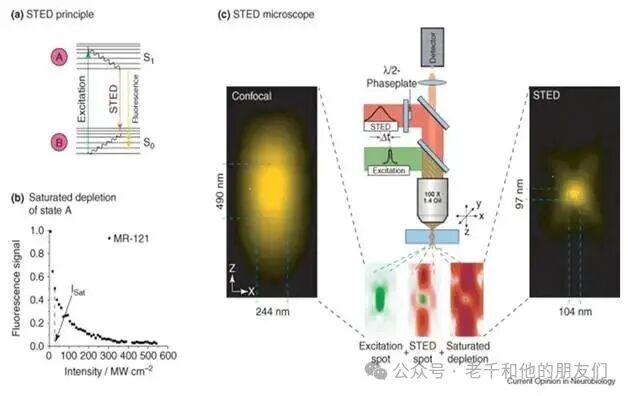
图 3:a 图:用绿光将电子从基态(S0)激发到第一激发单线态(S1),随后要么通过发射黄光回到基态(S0),要么通过 STED(黄光)作用回到基态;b 图:利用 STED 耗尽第一激发单线态(S1)的荧光团;c 图:左图为无 STED 时,焦平面内 z 方向与 x 方向的黄色荧光密度;中图上半部分为 STED 显微镜结构示意图,下半部分依次为 “无 STED 的绿色激发”“低强度红色 STED 与绿色激发光斑”“高强度红色 STED 与绿色激发光斑”;右图为高强度 STED 作用下的黄色荧光光斑。
通过这种设计,再结合激发光束与STED光束的最佳脉冲序列,除了衍射极限聚焦区域中的一小部分,其他区域的荧光发射都会被关闭。而且,随着STED光束最大强度(I0)的增加,这一小片荧光区域的尺寸会无限缩小。横向平面中有效荧光区域的宽度(Δmin)可近似表示为(Hell,2004):
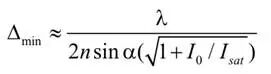
从这个公式能明显看出,阿贝判据带来的分辨率极限已被打破:随着I0无限增大,分辨率参数Δmin会趋近于零。实际上,当I0足够大时,受照区域将无限接近狄拉克函数(见图 4)。
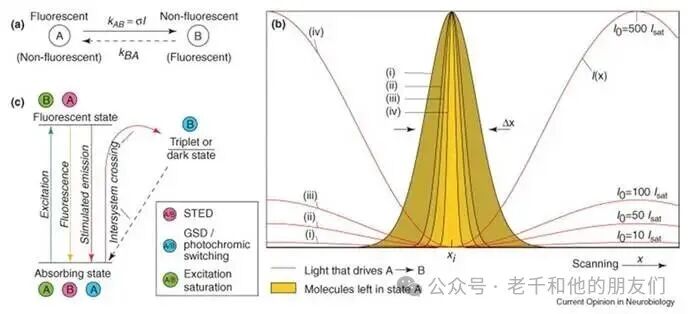
图 4:a 图:荧光损耗原理示意图;b 图:不同最大强度(I0)的 STED 强度(I (x),红色)下,焦平面内 x 坐标对应的荧光密度(黄色)。随着I0增大,荧光密度(黄色)会变得更锐利。
借助 STED 技术,原本受衍射极限限制的聚焦光斑可变得无限小。当然,高强度 STED 光束也可能带来其他问题,比如对生物组织的光损伤,但关键在于:这些问题并非由 “硬性物理极限” 造成,因此有望逐步解决 —— 例如,可采用除受激发射外的其他基态损耗机制,这类机制不需要如此高的光束强度(Hell & Kroug, 1995)。
黑尔团队首次验证 STED 原理的实验结果(Klar,2000),如图 5 所示,从中能清晰看到:轴向分辨率从约 500 纳米提升到了100 纳米,彻底改善了轴向分辨率差的问题。
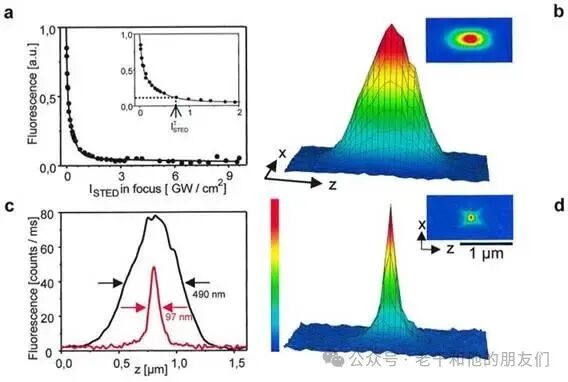
图 5:。a 图:荧光强度随 STED 强度(ISTED)的非线性下降;b 图:无 STED 时,x 方向与 z 方向的荧光强度光斑示意图;d 图:有 STED 时,x 方向与 z 方向的荧光强度光斑示意图;下方曲线为无 STED(黑色)和有 STED(红色)时,z 方向的实测荧光分布。
五年后,M. 古斯塔夫松(M. Gustafsson)利用 SSIM 技术实现了超分辨成像(Gustafsson, 2005)。令人惋惜的是,他于 2011 年不幸离世,这项研究也因此过早中断。
3.2 致密介质中单荧光团检测的艰难历程
尽管 “分子存在且其作用方式具有随机性” 这一观点早已得到认可((Einstein,1905),但 “化学反应是遵循确定性规律的动态连续过程” 这一认知,在很长一段时间里仍占据主导地位。
直到研究人员观察到 DNA 结合荧光染料(溴化乙锭)在平衡态下的波动,这一认知才被打破。当时,W. W. Webb与合作者E. Elson、D. Magde开发了荧光相关光谱(FCS)技术,并利用涨落-耗散定理,估算出常温下荧光染料与双链 DNA 相互作用的动力学速率常数。
差不多同一时期,R. Rigler及其团队提出,可通过荧光强度波动研究分子的旋转运动与荧光寿命(Rigler, 1974)。
几年后,T. Hirschfeld用聚乙烯亚胺将大量荧光团(每个蛋白质分子连接 80-100 个)标记到抗体(γ 球蛋白)上(Hirschfeld, 1976)。随后,他利用全内反射荧光(TIRF)显微镜,在常温下观察到这些多标记抗体在氩离子激光照射的小体积内,既会发生扩散运动,也会产生机械驱动的运动。这些通过 “近场激发+远场检测” 显微镜获得的结果,标志着 “致密介质中单荧光团检测” 这一艰难探索的开端。
W. E. 莫纳(W. E. Moerner)的团队首次在致密介质中观测到单个荧光团(Moerner & Kador, 1989)。他们在液氦温度(4K)下,测量了对三联苯晶体中单个并五苯分子非均匀展宽光学跃迁的统计精细结构。这一成果极具革命性 —— 尤其难得的是,莫纳团队并非通过光子发射,而是通过光子吸收来检测单个荧光团。这一发现直接证明了 “检测单个荧光团” 的可行性,也极大地推动了单分子领域的发展。
次年,M. 奥里特(M. Orrit)使用与莫纳团队相同的实验系统,测量了单个荧光团的荧光。不出所料,与基于吸收的观测相比,这种基于发射的方法信噪比大幅提升(Orrit & Bernard, 1990)。同年,R. A. 凯勒(R. A. Keller)与 R. 里格勒(R. Rigler)的团队在室温液体介质中检测到了单个荧光团:为了抑制背景辐射,里格勒团队采用了共聚焦显微镜技术,凯勒团队则用了 “脉冲激发+延迟光子检测” 的方法。
1993年,埃里克・贝齐格(Eric Betzig)利用近场扫描显微镜,以超分辨分辨率研究了风干表面上的单个荧光团。1994 年,R. A. 凯勒团队与S. Xie团队分别测量了单个荧光团的激发态寿命;同年,S. Nie、D. Chiu与 R. Zare在一项极具影响力的研究中,用共聚焦显微镜实现了单个荧光团扩散的检测(Nie 等,1994)。
1995 年,柳田敏雄(Yanagida)团队用 TIRF 显微镜记录到单个荧光标记的 ATP 分子与单个肌球蛋白分子的相互作用,这也成为单分子光谱学领域的又一里程碑(Funatsu 等,1995)。
总结来看,这些成果共同为单分子光谱学与单分子显微镜的发展铺好了道路。其中,马格德、埃尔森与韦伯的工作极具概念意义 —— 他们通过实验证明了化学反应中的波动现象,并利用涨落 - 耗散关系确定了反应速率常数;赫希菲尔德则通过 TIRF 激发与远场检测,观察到带多个荧光标记的单个抗体分子的运动,这一早期成果也预示了后续二十年的研究方向。
而莫纳团队在低温下首次检测到单个荧光团,更是决定性的突破 —— 它证明了 “看似不可能的事” 其实可行,不仅启发奥里特团队在低温下通过荧光检测单个荧光团,也为凯勒、里格勒、柳田敏雄等团队在 “常温液体介质”(生物研究的关键条件)下检测单个荧光团提供了重要参考。
3.3 超分辨单荧光团显微镜:PALM、STORM、PAINT 及其衍生技术
本文所说的 “超分辨单荧光团显微镜”,是指通过 “超定位” 光子点光源来实现超分辨成像的一类技术。正如前所述,来自点光源的光子到达显微镜探测器时,其空间概率密度由点扩散函数(PSF)决定(见图 6)。
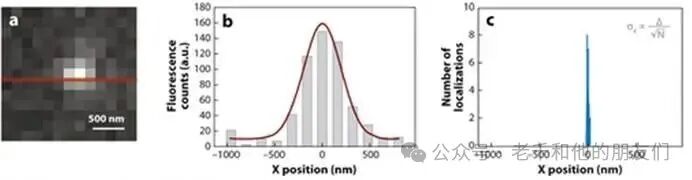
图 6:a 图:探测器 x 方向与 y 方向上单个荧光团的像素化荧光强度;b 图:x 方向的荧光强度(蓝色柱)拟合为正态分布(红色线,公式 4);c 图:(b) 中正态分布中心(x=0)的概率密度。已知存在单个发射体时,点光源位置的估算精度(c)远高于点扩散函数的宽度(b)。
若忽略背景与像素化的影响,横向平面中光子检测的概率密度p(x,y)近似呈高斯分布(Thompson ,2012):
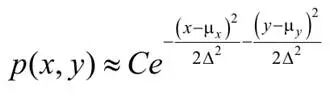
式中,C为归一化常数,μx与μy定义了点扩散函数(PSF)的横向中心,Δ与上述公式 1 中的阿贝衍射极限相等。
由于已知探测器上的光子分布来自单一光源,因此可估算点扩散函数的中心,其在 x、y 两个坐标方向上的标准误差(Δmin)为(Bobroff, 1996;Webb, 2002):
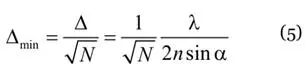
式中,N为探测器记录的光子总数。由此可见,显微镜的空间分辨率(即对点光源的定位能力,用Δmin表示)相较于阿贝原始极限,提升了1/N倍。
这意味着:若能从单个点光源检测到 100 个光子,Δmin会比阿贝极限小 10 倍;且随着检测光子数量的增加,分辨率的提升不存在严格限制。
不过,要实现这一点,需满足一个前提:感兴趣结构上的荧光团标记必须足够稀疏,确保荧光团之间的间距大于衍射极限。但这又带来了新问题 —— 根据 H. 奈奎斯特(H. Nyqvist, 1928)与 C. E. 香农(C. E. Shannon, 1948)的采样定理,要重建出分辨率为Δmin的结构,需以高于2/Δmin的空间频率对结构进行均匀采样。这一要求与 “荧光团最近邻距离大于阿贝衍射极限” 的前提相互矛盾。
实际上,要解决这一矛盾,需要满足两个看似对立的条件:一方面,荧光标记需足够稀疏,确保所有荧光团都是可区分的点光源;另一方面,荧光标记又需足够密集,以满足奈奎斯特与香农采样定理。埃里克・贝齐格(Eric Betzig)首次从概念上解决了这一逻辑难题。
尽管贝齐格在近场荧光显微镜领域的研究取得了成功(如 Betzig 等,1992;1993),但他逐渐意识到:这种技术局限于表面研究,且操作复杂,应用范围有限。于是,贝齐格暂时离开学术领域,但仍在思考超分辨荧光显微镜的突破方向。最终,他提出了一种新方法,既能实现超分辨成像,又能克服近场显微镜的缺陷(Betzig, 1995)。
他的思路是:分两步确定具有可区分光谱特性的大量点光源的位置。第一步,分别确定每类光谱荧光团的点扩散函数(PSF)—— 只要确保每类荧光团在空间上呈稀疏分布,就能通过公式 5 的精度估算其点扩散函数中心,实现超分辨定位;第二步,将所有类别荧光团的位置整合,即可得到对密集采样结构的超分辨图像。
后来,G. J. 布拉肯霍夫(G. J. Brakenhoff)团队在实验中采用了这一方法的一种具体形式,但当时仍未找到实现贝齐格设想的最佳实验方案。
贝齐格提出这一设想两年后,莫纳(Moerner)开始研究Roger Tsien团队提供的绿色荧光蛋白(GFP)突变体的发光特性。这些实验在常温下进行,将蛋白质嵌入充气水凝胶中(Dickson ,1997)。意外的是:当用 488 纳米波长的光激发时,这种蛋白质会出现多次间歇性荧光发射 —— 也就是 GFP 分子的 “闪烁”(blinking)行为。经过多次闪烁后,分子会进入稳定的暗态;更令人意外的是,用 405 纳米波长的光照射,又能将其从暗态重新激活。
这一发现首次证明:通过巧妙利用蛋白质自身的光化学特性,可实现荧光蛋白在 “活性态” 与 “非活性态” 之间的光学调控(见图 7)。
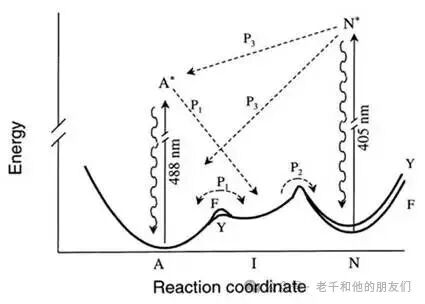
图 7:GFP 在 A 态时,被 488 纳米光激发至 A态,随后通过发射光子回到 A 态;若从 A 态进入中间态 I,会停止发射荧光,直至 I 态自发回到 A 态(即 “闪烁”);若从 I 态进入暗态 N,同样停止发射荧光,需通过 405 纳米光激发将 N 态激活至 N态,GFP 才能回到 A 态。(Dickson ,《Nature》, 1997)。
莫纳团队对 GFP “闪烁”与“光激活” 特性的发现,为探索 GFP 突变体的新型光学特性打开了大门。后来,J. 利平科特 - 施瓦茨(J. Lippincott-Swartz)团队开发出一种特性独特的 GFP 变体(Patterson & Lippincott-Schwartz, 2002):这种突变体初始时无光学活性,需通过 413 纳米光照射激活;激活后,在 488 纳米光激发下会发射荧光;最终,在 488 纳米光的强照射下,会因光漂白而不可逆失活。
贝齐格离开近场显微镜研究、短暂投身企业后,重新回到学术领域。当他了解到利平科特-施瓦茨团队发现的这种 GFP 突变体时,立刻意识到:这或许能解决 “如何将稀疏荧光团集合与密集总荧光团集合结合” 的难题。
解决方案其实很简单:用低强度 413 纳米光照射,在生物结构中激活极少量、呈稀疏随机分布的 GFP 突变体分子;随后用 488 纳米光照射,根据上述公式 5 的精度,对这一稀疏子集的分子进行超分辨定位;当第一子集因光漂白失活后,再激活第二个稀疏子集,对其分子进行高分辨率定位;以此类推,直到所有子集都被采样,最终得到真实的超分辨结构图像。
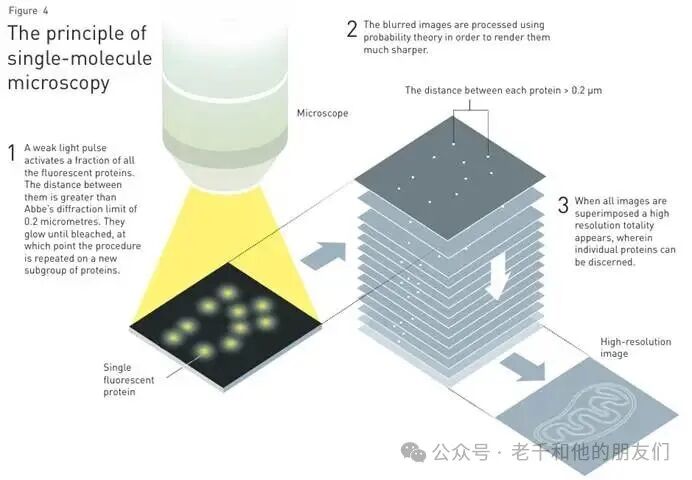
图 | 单分子显微镜原理
1.弱光脉冲激活部分荧光蛋白,它们彼此间距大于 0.2 微米的阿贝衍射极限;这些蛋白发光直至荧光消失,随后对新的蛋白亚群重复上述过程。
2.显微镜记录单个荧光蛋白的位置。
3.通过概率论处理模糊的原始图像,使其变得更清晰。
4.叠加所有图像,得到能分辨单个蛋白的高分辨率完整图像。
这种方法既满足了 “每次仅观察稀疏子集” 的要求,又能通过多次采样实现 “高频(密集)空间采样”,从而符合奈奎斯特与香农定理(见图 8)。
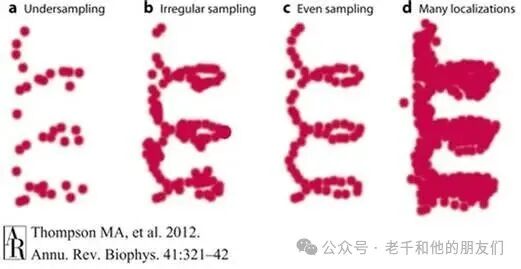
图 8:a 图:低频空间采样;b 图:偏倚采样;c 图:均匀采样;d 图:过采样。
贝齐格与利平科特 - 施瓦茨(Lippincott-Schwarz)、H. F. 赫斯(H. F. Hess)合作,将一种光激活绿色荧光蛋白(PA-GFP,如 Kaede 蛋白,与 Patterson & Lippincott-Schwartz 于 2002 年描述的蛋白类似)与溶酶体跨膜蛋白(CD63)融合表达,最终获得了固定哺乳动物溶酶体薄切片的超分辨结构(Betzig 等,2006),如图 9 所示。
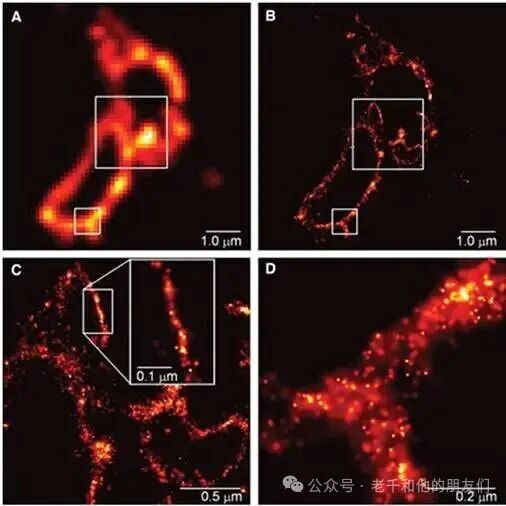
图 9:A 图:无 PALM 技术时,GFP 标记溶酶体蛋白(CD63)的分布;B 图:有 PALM 技术时,该蛋白的分布;C 图:B 图中方框区域的高倍放大图;D 图:B 图中小方框区域的高倍放大图。注:D 图中的比例尺接近阿贝极限。Betzig ,《Science》, 2006。
他们将这种方法命名为 “光激活定位显微镜(PALM)”。同年晚些时候,庄小威(X. Zhuang)团队(Rust ,2006)与 S. T. 赫斯(S. T. Hess)团队(Hess, 2006)分别发表了基于类似原理的超分辨荧光显微镜研究,并将各自的方法命名为 “随机光学重建显微镜(STORM)” 与 “荧光光激活定位显微镜(fPALM)”。
此外,R. M. 霍希施特拉瑟(R. M. Hochstrasser)团队也提出了另一种超分辨成像策略(Sharonov & Hochstrasser, 2006):利用荧光标记(尼罗红,Nile Red)与细胞内靶点(疏水膜)结合后荧光参数(发射光谱偏移)的变化实现超分辨,这种方法被命名为 “纳米级地形成像点累积显微镜(PAINT)”。此后,科研人员还开发了多种调控活性荧光团浓度的方案(Thompson 等,2012)。
4. 之后的发展
超分辨荧光显微镜的发展历史并不算长:基于集合荧光团的 STED 显微镜于 2000 年实现,基于单荧光团的超分辨显微镜于 2006 年问世。尽管如此,这类技术(如 Sahl & Moerner, 2013)发展迅速,如今已在细胞生物学、微生物学、神经生物学等生物科学核心领域广泛应用。
目前有充分理由相信,这一领域的发展(已产出大量此前无法获得的新颖成果)将在未来几十年加速推进。预计这一技术革命将深刻改变生物学与医学领域 —— 尤其是,它最终有望在纳米级分辨率下,对 “定义所有生命形式表型的复杂多维分子生物学过程” 进行真实、定量的动态描述。
参考资料Måns Ehrenberg SUPER-RESOLVED FLUORESCENCE MICROSCOPY

